WARNING : this idea has a current status of "failed idea" due to bad economics. But may be someone can transformed it into a good idea...
Le développement de l'énergie éolienne pose des questions sur son intégration dans le système énergétique existant. L'intermitance de la production et la concentration des zones de production dans des régions mal déservies par le réseau électrique sont par exemple des freins à son développement. De même, dans les systèmes électriques insulaires, l'énergie éolienne n'est pas l'énergie miraculeuse dont les îles ont besoin.
La valeur de l'énergie éolienne pour un système électrique est faible en raison de son imprévisibilité qui oblige le programmateur système à prévoir dans tous les cas une énergie de substitution qui pourra être sollicitée ou annulée à l'échelle de la prévision météorologique.
On propose dans ce projet une solution simple qui, au prix d'une perte de rendement énergétique, permet de diminuer les inconvénients de l'énergie éolienne. La solution ? Le stockage de l'énergie éolienne au fond des mers !
1 - Dimensionnement du stockage
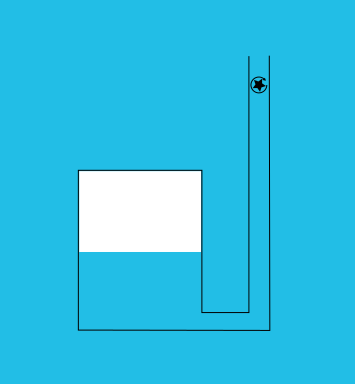
Le principe du projet est de stocker de l'air comprimé au fond de la mer dans une structure maintenue au fond par un ballast dimensionné en conséquence. La profondeur de stockage est une des grandeurs caractéristiques du système. La profondeur de stockage est \(H=\) 3000. A cette profondeur, la pression hydrostatique est égale à \(P=\) =[profondeur]*[densiteEau]*9.8/100000.
2 - Energie stockée
L'étude de dimensionnement utilise comme variable principale, l'énergie potentielle stockée. On prend comme hypothèse \(E=\) 100. En conséquence, le volume d'air immergé : \(V_2=\) =[energieStockage]*3600*1000000/[pression]/101325.
3 - Dimensionnement du stockage et du ballast
Le volume de stockage est maintenu au fond de la mer par un ballast dont les caractéristiques sont déterminées par l'équation d'équilibre suivante :
$$(\rho_B-\rho_E) V_B <= (\rho_E-\rho_A) V_2$$avec \(\rho_E\) la masse volumique de l'eau, \(\rho_A\) la masse volumique de l'air et \(\rho_B\) la masse volumique du ballast.
4 - Caractéristique du ballast
La densité de l'acier est de 7000 kg/m3, le sable 1500, le beton environ 2000 à 2500. Il existe également des bétons lourds à base magnétite ou hématite dont la densité peut atteindre 3500 à 5000. On suppose que la densité du ballast est \(\rho_B=\) 2000. En conséquence, la masse du ballast est =([densiteEau]-[densiteAir])/(1-[densiteEau]/[densiteBallast])*[volumeStokage]/1000 et son volume est =[masseBallast]/[densiteBallast]*1000.
On suppose un prix du béton de 70, soit un investissement de =[prixBeton]*[volumeBallast]/1000.
5 - Caractéristique de l'eau de mer
La densité de l'eau augmente approximativement d'un kg/m3 lorsque la température diminue de 5° C, la salinité augmente de 1 PSU ou la pression augmente de 20 bars. Avec les conditions retenues, on a \(\rho_E=\) =1000+[profondeur]/200.
6 - Caractéristique de l'air immergé
A la pression de travail, la densité de l'air comprimé est calculée par l'équation des gaz parfaits : \(\rho_A=\) =[pression]*28.95*100000/8.314/273/1000.